In order to render fluids in webGL from particles simulations, an implicit surface method has to be used to create a mesh from a point cloud that represents the current state of the simulation on each frame. To do so there are many algorithms that can be applied, being the Marching Cubes a good approach for webGL since its implementation can take advantage of histopyramids to accelerate the process in the GPU.
This algorithm is an iso surface extraction method from a potential field that uses a divide and conquer process locating the surface inside a user defined 3D grid structure (voxels), generating triangles where the iso surface intersects the voxels of the 3D space. The intersection of the iso surface with each voxel can be defined by the cut of each of the edges from the cube that represents the voxel.
The algorithm checks the value of the two vertices that define the edge in order to check if one of the edges from the voxel has been crossed by the surface. If the two vertices are below or above the iso surface value the edge hasn’t been crossed, on the other hand if one of the vertices is below and the other vertex is above, the edge has been crossed by the iso surface.
Each crossed edge from the voxel generates a vertex position that will be part of one of the triangles to create in the corresponding cube, and since there are a limited amount of edges a finite amount of triangles positions can be defined, being a total of 256 possible combinations present in the algorithm with up to five triangles per voxel. The final vertex position between the two borders is evaluated based on a linear interpolation of the potential value from the two vertex of the edge, using the iso surface value as the input parameter for the interpolation.

The first image (taken from http://paulbourke.net/geometry/polygonise/) shows the vertices and edge numbering convention used for the marching cubes, and the second image shows how one voxel is crossed by the iso surface in the edges 11, 2 and 3, generating a set of three vertices in the edges commented, the triangle generated is allocated on those three vertices obtained.
Since the calculation of each vertex position can be done individually the process can be easy parallelized using the GPU. Also the total amount of vertices to generate can be obtained in advance, this allows to allocate the required memory to generate the geometry, since the process relays heavily on tables that define the amounts of vertices per voxel.
A common approach to implement the marching cubes algorithm in the GPU is to use geometry shaders since the method is expected to generate a set of vertices from a single voxel query, this represents a big limitation in webGL because the current pipeline only supports vertex and fragment shaders. To overcome this impediment histopyramids can provide an effective way to allocate the required vertices needed to create the triangles.
The complete process for the surface generation can be separated in three different blocks, which are the potential generation, active voxels evaluation and finally the generation of the corresponding vertices positions with its normals for the triangles to render. This three blocks are defined in the following diagram.

3D Voxels Compacted Texture Generation
The marching cubes algorithm requires a potential field that has to be generated from the particle cloud. This is done using a separable blur that spreads the particle data generating the required potentials, the resulting blur creates a simulated non signed distance field blurring in the 3 main axes where the coefficients and the the radius of the blur control the smoothness of the surface.
Since the blurring process is a quite demanding step it can become the bottleneck of the surface generation, it all depends on the size of the 3D texture used to allocate the voxels where the particles reside. In order to improve the performance of the blurring process a 3D compacted texture is generated, using the RGBA channels of the texture to compress the different depth buckets of a conventional 3D texture.
The idea is to take advantage of the vector capabilities of the GPU to place all the voxel data in the four channels of each fragment, that would allow to blur the 3D texture on a smaller texture size. As an example a 256^3 texture can be simulated on a 4096×4096 non compressed 2D texture, where the space will be segmented in 256 buckets of 256×256 pixels.
The previous texture can be compressed using a 2048×2048 2D texture where the “R” channel holds the 256×256 size buckets which depths are between [0-64), the “G” channel holds the buckets which depths are between [64-128), the “B” channel holds the buckets which depths are between [128-192) and the “A” channel holds the buckets between depths allocated in [192-256).
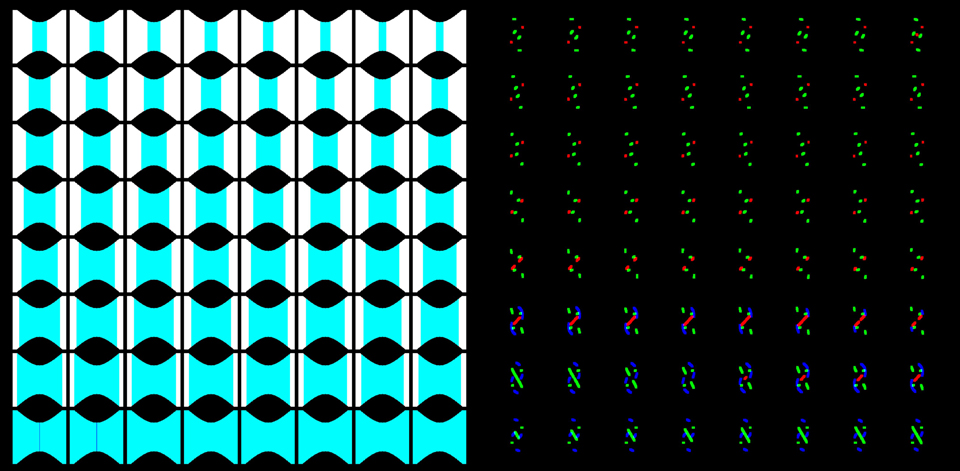
The image above shows two examples of a 256^3 compacted 3D textures. A simple inspection shows 64 (8X8) buckets of 256×256 pixels, where the depths can be read counting the bucket position and the corresponding RGBA color displayed. Notice that the same 2D position can represent more than one bucket (left 3D texture), in this case the white pixels represent that there’s a voxel with data for all the four depths encoded in those fragments.
A scattering program is written to populate the 3d texture where the vertex shader is responsible to allocate the particles inside the texture, and the fragment shader only assigns the corresponding color to each fragment. The following shaders are used to generate the required program
Vertex shader:
attribute vec2 aVertexIndex2D;
//Texture holding the positions of the particles from the simulation.
uniform highp sampler2D uPositionTexture;
//Size of the particle to draw in the 3d texture.
uniform float uSize;
//Displacement on the main axis to simulate the size of the particle in 3D
uniform float uDesface;
varying vec2 vV2I;
varying vec3 vPos;
//Constants used to simulate the 3D texture
const vec4 c3D = vec4(1. / 2048., 256., 8., 1. / 8.);
varying vec4 vColor;
void main(void) {
//obtain the position from the particle in [0-1] space.
vPos = texture2D(uPositionTexture, aVertexIndex2D).rgb;
//Define the 3D position in voxel space [0-256].
vec3 gPP = floor(vPos * c3D.y);
//Displace the main axis position to simulate a cube particle in 3D
gPP.y -= uDesface;
//Obtain the corresponding 2D position for the 2D texture.
vec2 gP = c3D.x * (gPP.xz + c3D.y * vec2(mod(gPP.y, c3D.z), floor(gPP.y * c3D.w)) + vec2(0.5));
//This defines the corresponding depth of the particle, it’s used to encode it in the
//corresponding channel.
float zLevel = floor(gP.y);
gP.y = fract(gP.y);
gP = 2. * gP – vec2(1.);
//The color of the channel depends on the corresponding depth of the particle.
vColor = vec4(equal(vec4(zLevel), vec4(0., 1., 2., 3.)));
//Set the size of the particle to render.
gl_PointSize = uSize;
gl_Position = vec4(gP, 0., 1.0);
}
Fragment shader:
varying vec4 vColor;
void main(void) {
}
The vertex shader uses the attribute aVertexIndex2D to define the UV required to read the 3d position of each particle represented as a vertex, these positions are saved in the uPositionTexture uniform. The uniform uSize is used to define the size of the particle in the voxel space, this is useful when there’re not too many particles in the simulation, or the geometry to generate is based on filaments generated from particles.
The constant c3D is a vector that is used to allocate the data in buckets that simulate the array of depths from a 3D texture. The corresponding channels are defined below:
c3D.x: inverse of the size of the texture 2D used to simulate the texture 3D (usually 1024 or 2048).
c3D.y: bucket side size for the texture3D simulated (usually 128 from 128^3 or 256 from 256^3)
c3D.z: number of buckets allocated in the horizontal row from the 2D texture. Usually 8 or 16 buckets.
Since the particles can have sizes bigger than one pixel, it’s required to represent them as cubes in the 3D texture. To do so the vertex shader uses the uOffset uniform, this value represents the displacement in the depth axis (in units) that the shader should offset to render the particle. This would represent the cube using the different slices to represent the size in 3D.
This means that the program has to be invoked as many times as the size of the particles, incrementing the value of uOffset on each pass to render the corresponding slices of the particle’s cube in the 3D texture.
One depth value is saved in the variable zLevel to define which channel will be used, since only 64 buckets can be represented per channel the zValue will define a value from [0-4). If the zValue is 0 the corresponding voxel will be encoding in the “R” channel, for a zValue of 1 the “G” channel is used, for zValue equal of 2 the “B” channel is used. Finally for a zValue of 3 the “A” channel holds the corresponding voxel.
3D Blur for Potential Field Generation
Once the 3D texture is filled with the particles a second program is required to generate the potentials using a 3D blur. This is done using a quad pass, and two different fragment shaders, one for the blur corresponding the non depth axis, and another fragment shader for the blur corresponding the depth axis. The fragment shader for the depth axis is defined below.
precision highp sampler2D;
uniform sampler2D uDataTexture;
uniform float uSteps;
varying vec2 vText;
//strength of the pixel to blur agains the other ones used.
const float coeficient = 2.;
const vec4 c3D = vec4(1. / 2048., 256., 8., 1. / 8.);
const float border = 1.;
//Evaluates the 2d index value in the simulated 3D texture from the 3D pos.
vec2 index2D(vec3 pos) {
}
void main(void) {
vec2 pos = floor(vText / c3D.x);
vec3 pos3D = vec3(mod(pos.y, c3D.y), c3D.z * floor(pos.y / c3D.y) + floor(pos.x / c3D.y), mod(pos.x, c3D.y));
vec3 newPos3D = vec3(0.);
vec2 uv = vec2(0.);
vec4 blend = vec4(0.);
float zLevel = 0.;
//Obtain the z level for the corresponding fragment.
float currentZLevel = floor(pos3D.y / 64.);
for (float i = 0.; i <= 40.; i ++) {
float j = i – uSteps;
//Obtain the new 3D pos of the fragment to use for blurring.
newPos3D = pos3D + j * vec3(0., 1., 0.);
//Obtain the z level for the new fragment to read.
zLevel = floor(newPos3D.y / 64.);
uv = index2D(newPos3D);
uv.y = fract(uv.y);
float k = j == 0. ? coeficient : 1.;
vec4 newBucket = texture2D(uDataTexture, uv);
//If the new fragment is in the same depth range than the original fragment to blur then the same channels are used.
//If the new zLevel is different than the current Z level the blurring have to be done taking into account the
//channel differences between the two fragments.
vec3 cases = vec3(bvec3(zLevel < currentZLevel, zLevel == currentZLevel, zLevel > currentZLevel));
blend += k * (vec4(0., newBucket.rgb) * cases.x + newBucket * cases.y + vec4(newBucket.gba, 0.) * cases.z);
}
blend /= (2. * uSteps + coeficient);
//This avoids to spread information between the different buckets.
blend *= float(mod(pos.x, 256.) > border && mod(pos.y, 256.) > border && mod(pos.x, 256.) < 255. - border && mod(pos.y, 256.) < 255. - border);
gl_FragColor = blend;
}
Fragment shader for two non depth coordinates blur:
precision mediump sampler2D;
uniform sampler2D uDT;
uniform vec3 uAxis;
uniform float uSteps;
varying vec2 vText;
const float coeficient = 2.;
void main(void) {
for (float i = 0.; i <= 40.; i ++) {
float j = i – uSteps;
float k = j == 0. ? coeficient : 1.;
blend += k * texture2D(uDT, vText + j * uAxis.xy);
}
blend /= (2. * uSteps + coeficient);
gl_FragColor = blend;
}
Since the 3D texture is simulated using contiguous buckets in the 2D texture, the blur for the depth axis has to take into account the depth range for every fragment used in the blurring process, hence a vector is defined to know if the depth of the fragment to use is in the range of the depth from the fragment to blur. There are three different scenarios depending on the two depth values (fragment to blur “currentZLevel” and fragment to use for blurring “zLevel”), these are defined below.
if zLevel is equal than the currentZlevel, the original channels are blended with the new channels with the following equation blend += newBucket.rgba.
If zLevel is below the currentZlevel, the original channels are blurred with the new data using the following equation… blend += vec4(0, newBucket.rgb).
if zLevel is over the currentZlevel, the original channels are blurred with the new data using the following equation… blend += vec4(newBucket.gba, 0).
The three previous scenarios are used to match the compressed RGBA data between the two values, these equations are not necessary for the two other axis (non depth ones) since the blurring is done inside the same depth bucket.
For the non depth axis a simple box blur is used defining the blurring direction based on a user provided uniform uAxis, this allows to make the 3D blur in three different separable passes. Notice that the filtering done is based on box coefficients, but these could be modified to make a gaussian filter or any type of filtering that could provide better results for the potential to simulate.
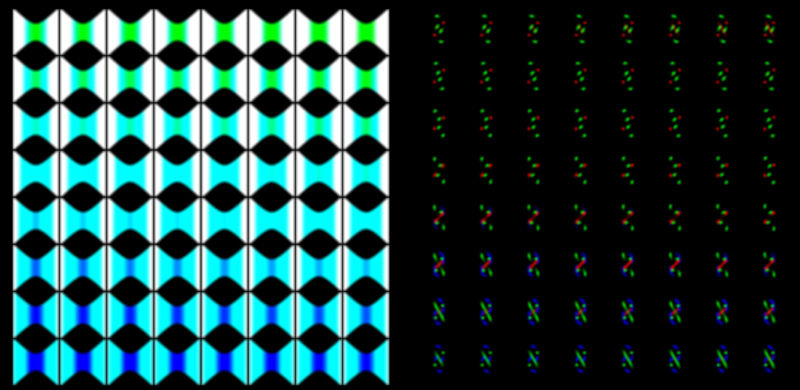
The following image shows the result of the potential generation for the two previous 3D textures, notice that for the left image the buckets are separated avoiding blurring between the buckets. It can be seen in the left 3D texture that the appearance of the green and dark blue colors show how the different depths are being blended, meaning that the potential is being softened among the different depths.
Corners Calculation in the Potential Field
Once the potential is obtained, the marching cubes algorithm requires to evaluate the values in the corners of the voxels. In order to avoid software trilinear interpolations another quad pass is done over the result from the 3D blur passes to calculate values in the corners. Since it’s a quad evaluation the same vertex shader from the previous passes can be reused, and the corresponding fragment shader for the program is defined below.
precision highp sampler2D;
uniform sampler2D uDataTexture;
varying vec2 vText;
vec3 data[7];
const vec4 c3D = vec4(1. / 2048., 256., 8., 1. / 8.);
vec2 index2D(vec3 pos) {
}
void main(void) {
vec3 pos3D = vec3(mod(pos.y, c3D.y), c3D.z * floor(pos.y / c3D.y) + floor(pos.x / c3D.y), mod(pos.x, c3D.y));
data[0] = vec3(-1., -1., -1.);
data[1] = vec3(0., -1., -1.);
data[2] = vec3(0., 0., -1.);
data[3] = vec3(-1., 0., -1);
data[4] = vec3(-1., -1., 0.);
data[5] = vec3(0., -1., 0.);
data[6] = vec3(-1., 0., 0.);
float currentZLevel = floor(pos3D.y / 64.);
vec2 uv = index2D(pos3D);
uv.y = fract(uv.y);
vec4 corner = texture2D(uDataTexture, uv);
vec3 newPos3D = vec3(0.);
float zLevel = 0.;
for(int i = 0; i < 7; i ++) {
zLevel = floor(newPos3D.y / 64.);
uv = index2D(newPos3D);
uv.y = fract(uv.y);
vec4 newBucket = texture2D(uDataTexture, uv);
vec3 cases = vec3(bvec3(zLevel < currentZLevel, zLevel == currentZLevel, zLevel > currentZLevel));
corner += vec4(0., newBucket.rgb) * cases.x + newBucket * cases.y + vec4(newBucket.gba, 0.) * cases.z;
}
gl_FragColor = vec4(corner * 0.125);
}
Notice that the corners evaluation is done using the compressed blurred texture from the previous pass, this means that the same blending equations have to be used to match the different channels based on the depths regions of the fragments to use. With this final pass the algorithm has two potentials textures, one for center values and other for corner values, this last one is the texture used for the marching cubes steps.
Voxel Potential Field Expansion
For the marching cubes steps it’s not necessary to work with a compressed texture, hence a expansion step is used to obtain a 3D texture where each voxel is represented using a single fragment from the new texture. This is also done using a fragment shader defined below.
precision highp sampler2D;
uniform sampler2D uDataTexture;
const vec4 c3D_h = vec4(1. / 4096., 256., 16., 1. / 16.);
const vec4 c3D_l = vec4(1. / 2048., 256., 8., 1. / 8.);
varying vec2 vText;
void main(void) {
vec2 pos = floor(vText / c3D_h.x);
vec3 pos3D = vec3(mod(pos.y, c3D_h.y), c3D_h.z * floor(pos.y / c3D_h.y) + floor(pos.x / c3D_h.y), mod(pos.x, c3D_h.y));
//Define the depth range for the corresponding fragment.
float zLevel = floor(pos3D.y / 64.);
vec2 uv = c3D_l.x * (pos3D.xz + c3D_l.y * vec2(mod(pos3D.y, c3D_l.z), floor(pos3D.y * c3D_l.w)) + vec2(0.5));
uv.y = fract(uv.y);
//Set the value of the fragment based on the depth and the corresponding channel.
gl_FragColor = vec4(dot(texture2D(uDataTexture, uv), vec4(equal(vec4(zLevel), vec4(0., 1., 2., 3.)))));
}
The previous shader expands a 3D compressed RGBA texture allocated in a 2048×2048 2D texture where the visual buckets are allocated in 8 x 8 array of 256×256 fragments buckets. The result is a 4096×4096 texture where the visual buckets are uncompressed into an array of 16 x 16 buckets of 256×256 fragments. The different constant values for the expansion are defined in c3D_h and c3D_l.
The shader evaluates the 3D position of the fragment in the expanded texture and search for that value in the compressed texture, using the depth range to define with RGBA channel will be read to obtain the corresponding information. The image below shows the result of the expansion from the texture.

The left side of the previous image shows the compressed data in a 2048^2 area, allowing to calculate the blur and corners evaluation much faster than using a non compressed data. A speed up to 4X is gained based on the fact that the compressed texture area is 4 times smaller than the non compressed one. The right side shows the expanded result where the 256 depth buckets can be inspected visually without color interpretations.
Once the potential is generated it’s time to obtain the active voxels to use for the marching cubes, and generate the corresponding vertices, this will be explained in a second post, finally a third post will explain the javascript implementation and provide different examples with it.
